龙格库塔法的稳定性分析

单步法的稳定性

基本概念

考虑一阶常微分方程的初值问题：

$$\frac{dy}{dt} = f(t, y), \quad y(t_0) = y_0$$

对于线性测试方程：

$$\frac{dy}{dt} = \lambda y, \quad y(0) = 1$$

其精确解为 $y(t) = e^{\lambda t}$。

绝对稳定性

设数值解为 $y_n \approx y(t_n)$，则单步法可以写成：

$$y_{n+1} = R(h\lambda) y_n$$

其中 $R(h\lambda)$ 称为增长因子或放大因子，$h$ 是步长。

定义：如果 $|R(h\lambda)| \leq 1$，则称该方法在 $h\lambda$ 处是绝对稳定的。

稳定域：使得 $|R(h\lambda)| \leq 1$ 的复平面上的区域 $S = \{z \in \mathbb{C} : |R(z)| \leq 1\}$。

常见方法的增长因子

显式欧拉法：$R(z) = 1 + z$
隐式欧拉法：$R(z) = \frac{1}{1-z}$
梯形法：$R(z) = \frac{1+z/2}{1-z/2}$

四阶龙格库塔法和增长因子

经典四阶龙格库塔法

经典的四阶龙格库塔法（RK4）为：

$$\begin{align} k_1 &= hf(t_n, y_n) \\ k_2 &= hf(t_n + h/2, y_n + k_1/2) \\ k_3 &= hf(t_n + h/2, y_n + k_2/2) \\ k_4 &= hf(t_n + h, y_n + k_3) \\ y_{n+1} &= y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) \end{align}$$

RK4的增长因子

对于测试方程 $y' = \lambda y$，RK4的增长因子为：

$$R(z) = 1 + z + \frac{z^2}{2} + \frac{z^3}{6} + \frac{z^4}{24}$$

其中 $z = h\lambda$。

稳定域分析

RK4的稳定域由不等式 $|R(z)| \leq 1$ 确定。通过数值计算可以得到：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import matplotlib.pyplot as plt

# 网格设置
x = np.linspace(-4, 4, 800)
y = np.linspace(-4, 4, 800)
X, Y = np.meshgrid(x, y)
Z = X + 1j * Y

# RK4 稳定性函数
R = 1 + Z + Z**2 / 2 + Z**3 / 6 + Z**4 / 24

# 稳定区域：|R(z)| < 1
plt.contourf(X, Y, np.abs(R) < 1, levels=1, colors=['blue'], alpha=0.5)
plt.contour(X, Y, np.abs(R), levels=[1], colors='black')
plt.title("RK4 Stability Region")
plt.xlabel("Re(z)")
plt.ylabel("Im(z)")
plt.gca().set_aspect('equal')
plt.grid(True)
plt.show()

png

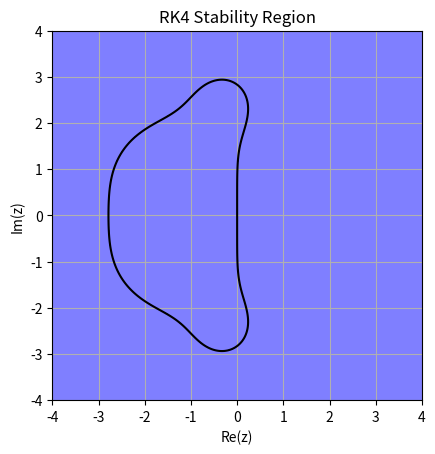
边界值大概为2.78左右。

在有限元中的应用

时间离散化

在有限元方法中求解抛物型偏微分方程时，空间离散化后得到常微分方程组：

$$\frac{d\mathbf{u}}{dt} = \mathbf{A}\mathbf{u} + \mathbf{f}(t)$$

其中 $\mathbf{A}$ 是刚度矩阵，通常具有负的特征值。

稳定性要求

设 $\mathbf{A}$ 的特征值为 $\lambda_i$，则稳定性要求：

$$h \max_i |\lambda_i| \leq \text{稳定域边界}$$

对于RK4，这意味着：

$$h \leq \frac{2.78}{|\lambda_{\max}|}$$

当矩阵 $\mathbf{A}$ 具有很大的负特征值时（刚性问题），RK4需要非常小的时间步长才能保持稳定，这会导致计算效率低下。

参考文献

以下文件由chatgpt给出，我并不保证文献的有效

Hairer, E., Nørsett, S. P., & Wanner, G. (1993). Solving Ordinary Differential Equations I: Nonstiff Problems. Springer.
Butcher, J. C. (2016). Numerical Methods for Ordinary Differential Equations. Wiley.
Hughes, T. J. R. (2000). The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Dover Publications.